singularity
- In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph
- Basic Classifications:
- Ordered Trees:
- Other Specialized Trees:
- B-Tree: A balanced tree designed for efficient storage and retrieval of data on disk.
- B+ Tree: Similar to B-Trees
- Trie: A specialized tree for storing prefixes.
- Segment Tree: A tree used to store information about intervals or segments on a line.
- heap aka priority queue: A tree-based structure where the root node has a specific property (e.g., largest or smallest value).
- Choosing the Right Tree:
- DB performance: binary, B, LSM trees
In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected graph
There are many types of trees in data structures, each with specific properties and use cases. Here’s a breakdown of some common ones:
Basic Classifications:
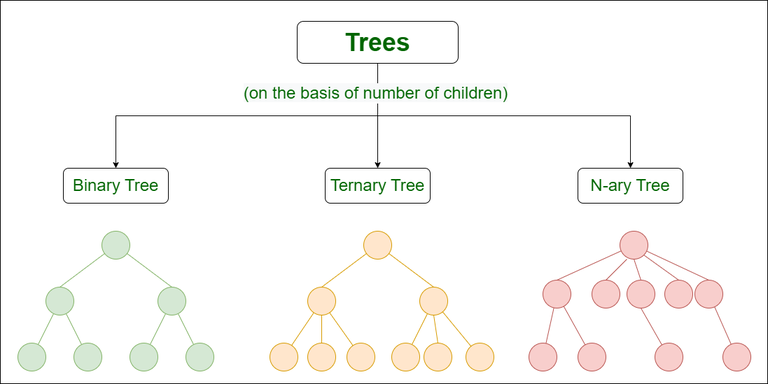
General Tree (N-ary Tree): The most general form, where a node can have any number of children.
Not very common in practice due to complexities in balancing and searching.
Binary Tree: Each node can have at most two children, typically referred to as “left” and “right.”
This is a fundamental structure for many other tree types.
Ordered Trees:
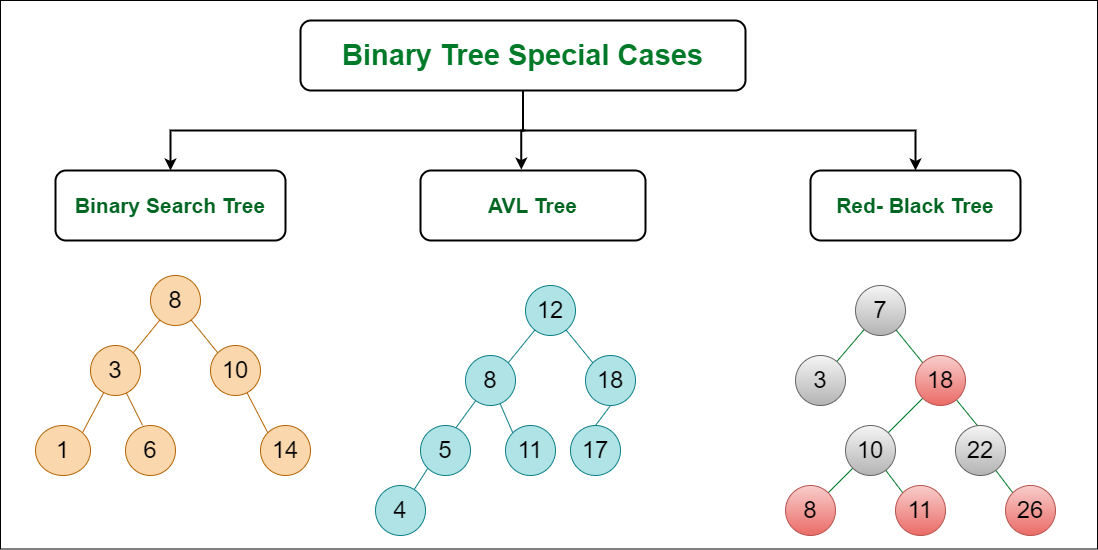
Binary Search Tree (BST): A binary tree where each node has a value greater than all its left children and less than all its right children.
This allows for efficient searching (average logarithmic time complexity).
AVL Tree: A self-balancing BST
that ensures the height difference between subtrees is always bounded, guaranteeing efficient searching and insertion operations.
Red-Black Tree: Another self-balancing BST
with similar properties to AVL trees, but with slightly different balancing rules.
Other Specialized Trees:
B-Tree: A balanced tree designed for efficient storage and retrieval of data on disk.
Commonly used in databases for indexing large datasets.
B+ Tree: Similar to B-Trees
but data is stored only in leaves, allowing for better space utilization and efficient range queries.
Trie: A specialized tree for storing prefixes.
Useful for applications like autocomplete or spell checking.
Segment Tree: A tree used to store information about intervals or segments on a line.
Efficient for performing range queries on the data.
heap aka priority queue: A tree-based structure where the root node has a specific property (e.g., largest or smallest value).
Used for priority queues and implementing efficient sorting algorithms.
Choosing the Right Tree:
The appropriate tree type depends on your specific needs. Here are some factors to consider:
- Ordering: Do you need the elements sorted (like in BST) or not?
- Search/Insertion frequency: How often will you be searching or inserting elements?
- Balance: Is self-balancing important for maintaining efficient operations?
- Data size and storage: Are you dealing with large datasets that need efficient storage and retrieval (like B-Trees)?
DB performance: binary, B, LSM trees
While binary trees are excellent data structures for many applications, they have limitations that make them less suitable for databases compared to B-trees and LSM-trees. Here are some reasons why:
Binary Trees:
- Balancing: Binary trees can become unbalanced, leading to poor search, insertion, and deletion performance. Self-balancing binary trees like AVL trees or red-black trees can mitigate this issue, but they come with additional complexity.
- Height: Binary trees can grow very tall, resulting in a large number of disk accesses, which can lead to poor performance in disk-based databases.
- Cache efficiency: Binary trees can exhibit poor cache locality, as nodes are not necessarily stored contiguously in memory, leading to slower access times.
B-Trees:
- Balancing: B-trees are designed to remain balanced, ensuring that search, insertion, and deletion operations have a logarithmic time complexity. This balance is maintained by splitting or merging nodes.
- Fanout: B-trees have a high fanout (i.e., many children per node), which reduces the tree height and improves cache locality.
- Disk efficiency: B-trees are optimized for disk storage, with each node representing a disk block. This leads to efficient use of disk space and reduces the number of disk accesses.
LSM-Trees (Log-Structured Merge-Trees):
- Write optimization: LSM-trees are designed for high write throughput, making them suitable for databases with high insertion rates. They achieve this by using a log-structured approach, where new data is written to a log, and then periodically merged into the main tree.
- Compaction: LSM-trees use compaction to remove unnecessary data and maintain a compact representation of the data, reducing storage requirements.
- Read performance: LSM-trees can provide good read performance by using a combination of caching and Bloom filters to quickly identify the location of data.
Why B-Trees and LSM-Trees are preferred in databases:
- Disk efficiency: Both B-trees and LSM-trees are designed to optimize disk accesses, reducing the number of disk I/O operations and improving overall performance.
- Balancing and tree height: B-trees maintain balance and a reasonable tree height, while LSM-trees use compaction to maintain a compact representation of the data.
- Cache efficiency: Both B-trees and LSM-trees exhibit good cache locality, reducing the number of cache misses and improving access times.
- Scalability: B-trees and LSM-trees can handle large amounts of data and scale well with increasing data sizes.
In summary, while binary trees are excellent data structures, their limitations make them less suitable for databases. B-trees and LSM-trees, on the other hand, are designed to address the specific challenges of disk-based databases, providing better performance, scalability, and efficiency.